Rubik PLL

This page is dedicated to permute correctly the last layer of the Rubik's cube.

The 21 PLL cases

Source:

• BB: Bob Burton's - cubewhiz.com (including original pictures and comments),
• BM: Badmephisto's algo,
• AK: Andy Klise's algo,
• VC: Victor Colin's algo.

Moves in BOLD are my current favorites.

Probabilities:

• BLUE — p=1/18
• GREEN — p=1/36
• RED — p=1/72

Permutations of edges or corners only

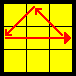Ua	(R2 U') (R' U' R U) (R U) (R U' R) (VC video) [y2] (R U' R U) (R U) (R U') (R' U' R2) (BB) BB:This is just a simple 3-edge cycle. It is almost as fast as the corner cycles. I solve this case with the bar at the front or the back. No AUF if front bar matches F face.		(R' U R' U') (R' U') (R' U) (R U R2) (VC video) [y2] (R2 U) (R U R' U') (R' U') (R' U R') (BB) 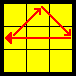BB:This is the inverse of the other U perm. I place my hands slightly differently for this algorithm. I solve this case with the bar at the front or the back. No AUF if front bar matches F face.	Ub
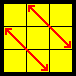Z	(M2' U) (M2' U) (M' U2) (M2' U2) (M' [U2]) (BB, VC Video) (M2' U') (M2' U') (M' U2') (M2' U2') (M' [U2']) (BB,VC,mirror) BB:The Z permutation is performed very similarly to the H perm. The last U2 is not necessary if you account for it before the algorithm. No AUF if front headlight is OPPOSITE to F face.		(M2' U) (M2' U2) (M2' U) M2' (BB, VC Video) (M2' U') (M2' U2') (M2' U') M2' (BB,VC,mirror) BB:This is extremely easy to recognize and can be performed VERY quickly. The M'2 is actually performed as (M'M') with rapid pushing at the back face of the M layer with the ring and then middle fingers. No AUF if front headlight matches F face.	H
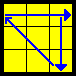Aa	x (R' U R') D2 (R U' R') D2 R2 (BB,VC video) BB:This is a basic corner 3-cycle. It is one of my favorite and fastest algorithms. Perform the D2s with the left hand and everything else with the right. To avoid a parasitic move of the L face after D2 (R ... that would block the U' move, the key is to twist slightly the right wrist such that to make a small D' move that would block the L face, hence stabilizing the cube. No AUF if front block matches F face.		x R2 D2 (R U R') D2 (R U' R) (BB,VC Video) BB:This is just the inverse of the other A perm. It is performed in a very similar manner. Same remark as for Aa. No AUF if front block matches F face. [y'] x (L U' L) D2 (L' U L) D2 L2	Ab
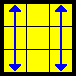E	x' (R U') (R' D) (R U R' D') (R U R' D) (R U') (R' D') (BB, VC Video) BB:This alg is just two orientations performed consecutively. Note:The algo are OCLL5 OCCL4. No AUF if edge centers match their face.			solved

Swap one set of adjacent corners

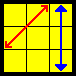Ra	R U R' F' R U2 R' U2 R' F R U R U2 R' [U'] (BB) BB:You could also just mirror Rb, but this alg is more right and friendly. Notice the similarity with the Jb permutation. (R U' R' U') (R U R) D (R' U' R) D' (R' U² R') (VC video) No AUF if front RIGHT CORNER matches F face.		(R' U2) (R U2) (R' F R U R' U') (R' F' R2 [U']) (BB, VC video) 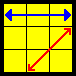BB:This is a pretty straightforward alg that flows pretty nicely. No AUF if front EDGE CENTER matches F face.	Rb
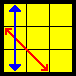Ja	(R' U L') U2 (R U' R') U2 (L R U') (BB) z (D' R U') R2 (D R' D') R2 (U D R') (BB,same with z setup) BB:I perform the R of the [R L] a split second after I start the L so that I can immediately perform the U' to AUF when the L face has been moved to where it belongs. (L' U' L F) (L' U' L U) (L F' L2' U L) (VC video VC) First F with RH index. No AUF if front FRONT BLOCK matches F face.		(R U R' F') (R U R' U') (R' F) (R2 U') (R' [U']) (BB) BB:This is the same as the T perm with the last four moves instead performed at the beginning. (R U R' F') (R U R' U') (R' F R2 U' R') (VC, edited from Ja perm) 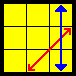First F with LH index. No AUF if front FRONT BLOCK matches F face.	Jb
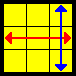T	(R U R' U') (R' F) (R2 U' R' U') (R U R' F') (BB,edited) BB:This is the T permuation. It is long but definitely very fast and easy. It can be performed in almost one swift motion without any readjusting of the fingers. Note that it is a combination of two easy orientations. No AUF if front FRONT BLOCK matches F face.		(R' U' F') (R U R' U') (R' F) (R2 U' R' U') (R U R' U R) (BB,edited) 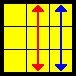BB:This is a T permutation with a 3 move setup in the beginning and a cancellation of one of those moves at the end. No AUF if front LEFT CORNER matches F face.	F

Swap one set of corners diagonally

.

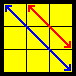V	(R' U R' d') (R' F' R2 U') (R' U R' F) (R F) (video VC) BB:This is one of my least favorite permutations because the flow just isn't there. No AUF if front block matches F face.		(F R U') (R' U' R U) (R' F') (R U R' U') (R' F R F') (BB) BB:This is very quick and can be performed without any adjustments of where the fingers are. It is just a combination of two quick orientations. First F' with the LH index (as for Jb perm). No AUF if front block matches F face.	Y
Na	(z) D (R' U) (R2 D' R D U') (R' U) (R2 D' R U' R) (BB) BB:This alg could also be performed using <R,U,L> if you don't do the rotation, but this way is faster with practice. z U (R' D) (R2 U' R U D') (R' D) (R2 U' R D' [R]) (cyotheking video) Normal grip after z. RH sexy regrip during the first and second U'. No AUF (last R if blocks on F and L faces are swapped. Otherwise, AUF taking in account that F and L blocks are swapped. (R U R' U) (R U R' F') (R U R' U') (R' F R2 U' R') (U2 R U' R) (VC, from youtube chat) Sexy grip star, with two variants: either second U with RH like a Sune, or pushed with LH index. No AUF if front block matches the F face.		(z) U' (R D') (R2' U R' D U') (R D') (R2' U R' D R') (BB) BB:This is just the mirror of the other N permutation. z U' (R D') (R2 U R' D U') (R D') R2 U R' D [R] (cyotheking video) Normal LH grip, RH sexy grip z. RH sexy regrip for both R2. All U, D' done with RH. (R' U R U') (R' F' U' F) (R U R' F) (R' F' R U' R) (VC video) Note:Looks easier to fingertrick. Always AUF FIRST, such that front block matches F face.	Nb

Double spins

To recognize these PLLs:

• Put the HEADLIGHT on the left
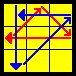
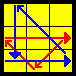
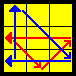
• Observe the position of the BLOCK: if it is as the FRONT (resp. FAR RIGHT, BACK and CLOSE RIGHT), then it is a Ga (resp. Gb, Gc and Gd) permutation.

To remember the algorithms, observe the sequence of RIGHT face versus sequence of UP face:

• Ga: R2 R' R' R vs u U U' u'
• Gb: R2 R' R R vs u U U' u' — Quick recognition: BLOCK is on the RIGHT on the face and next to OPPOSITE color!
• Gc: R2' R R R' vs u' U' U u
• Gd: R2' R R' R' vs u' U' U u — Quick recognition: BLOCK is on the LEFT on the face and next to OPPOSITE color! Also, the middle color in the PHARE is opposite (like for the Gb)

Ga	(R2 u) (R' U R' U' R u') R2' y' (R' U R) (BB,VC video) BB:This alg has a pretty decent flow to it and can be performed almost in one motion until the rotation. Right thumb on URB corner and right ring/major on F face. First u with RH index, and U with major/ring fingers. Then U' and u' with LH. No AUF if front block matches the F face.		[y'] (R' U' R) y (R2' u R' U) (R U' R u' R2') (BB) BB:This is the inverse of Ga. Note how similar they look. I perform this one almost exactly the same way. (F' U' F) (R2' u R' U) (R U' R u' R2') (VC, from an example solve) F' and F with RH thumb and index, then similar to Ga.	Gb
Gc	(R2' u' R U') (R U R' u R2) (f R' f') (bB) BB:You could rotate and insert the pair instead of performing the last three moves as shown. Start with RH thumb and index pinching RU corner-edge-corner (such that to be out of the way for the first u'), and RH ring finger under RD edge, and LH in standard grip. First u' with LH index or ring, which requires lifting slightly the RH index and ring fingers. During U' R, the RH thumb must move down such that not to block the U move done with RH index. The last u is done with the RH ring finger that was prepared from the beginning.) [y2] R2' F2' R U2 R U2') (R' F R U) (R' U' R' F) R2 (VC,example solve) Start with RH under D face and RH thumb on RU edge, F2' and U2 with RH index+middle, U2' with LH. No AUF if front block matches the F face.		[y] (R U R') y' (R2' u' R U') (R' U R' u R2) (BB) BB:This is just the inverse of Gc. I execute it very similarly because most of the moves overlap in the same manner. (f R f') (R2' u' R U') (R' U R' u R2) (VC video) Careful with regrip after R2' move. The RH ring finger must be under RD edge, and thumb on the FRD corner, such that at the u move the slice is pushed by the RH ring finger, and the thumb is holding the BRD corner and not the RD edge with a risk of lock because it would push the RD edge upwards.	Gd

PLL training sequence

From Victor Colin:

Ga	(R2 u) ...
Nb	(R' U R U') ...
Gb	(F' U' F) ...
Gd	(f R f') ...
Gc	(R2' u' R U') ...
Y	(F R U') ...
Ra	(R U' R' U') ...
Ua	(R2 U') ...
Rb	(R' U2) (R U2) ...
Ub	(R' U R' U') ...
Jb	(R U R' F') ...
F	(R' U' F') ...
V	(R' U R' d') ...
Na	(R U R' U) ...
Aa	x (R' U R') ...
Ab	x R2 ...
H	(M2' U') (M2' U2') ...
Z	(M2' U') (M2' U') ...
E	x' (R U') ...
T	(R U R' U') ...
Ja	(L' U' L F) ...

Recognizing the PLL cases

Links

• Recognizing the PLLs, from Badmephisto

A *must* see video on how to quickly recognizes the PLL based on features like headlights, bar, pairs...

• Recognizing the PLLs, from Bob Burton

2-face recognition

Code:

• X denotes same color. For instance, .X. X.. means a corner color matches the center color of adjacent edge.
• +- denotes opposite color. For instane, .-. +.. means a corner color is opposite to the center color of adjacent edge.

Features	Solved	Ua	Ub	Z	H	Aa	Ab	E	Ra	Rb	Ja	Jb	T	F	V	Y	Na	Nb	Ga	Gb	Gc	Gd
Two bars	4
Bar + pair											1	1
Bar + headlight		2	2
Bar only						1	1							2
Corner (same corner color)											1	1
Corner (2x opposite)															1
Two counter pairs																1
Two pairs (opposite + adjacent) (i.e. 3 colors)											2	2
Two pairs (2 x opposite) (i.e. 4 colors)																	4	4
One pair + shared headlight (opposite)													2
One pair + shared headlight (adjacent)									1	1
One pair + headlight (adjacent, 3 colors)						1	1
One pair + headlight (adjacent, 4 colors)																			1		1
One pair: ++-																						2
One pair: -++																				2
One pair (other cases)						1	1		1	1			2		2	2			1	2	1
Two headlights (2x opposite)					4
Two headlights (2x adjacent,2 colors)				2
Two headlights (2x adjacent,3 colors)		1	1
Two headlights (2x adjacent,4 colors)				2
Two headlights (adjacent + opposite)		1	1
One headlight						1	1		1	1									1	2	1	2
Nothing: .X- X+.								4
Nothing (other cases)									1	1				2	1	1			1		1

Draft

	Solved.
	Aa. The corner block + headlight, or corner block + opposite color on same face (telling where the headlights are)
	Ab. The corner block + headlight, or corner block + opposite color on same face (telling where the headlights are)
	E. No blocks. We see: orange green - orange blue on the corner → orange face must be on the left.
	Ua

Recognition

It's very easy to observe two sides. Depending on what you see, it will quickly narrow down the possible cases. The features to observe are:

• The bar: A side with 3 identical color.
• The corner: A corner with 2 adjacent edges of same color.
• The pair: A corner and an adjacent edge of same color.
• The headlight: Two corners of same color.

Two bars

• The cube is solved. Just AUL as necessary.

Bar + headlight

• Possible cases are: Ua or Ub
• Ua: if headlight on the right (resp. left) contains adjacent (resp. opposite) colors
• Ub: if headlight on the right (resp. left) contains opposite (resp. right) colors

Bar + pair

• Possible cases are: Ja or Jb.
• Ja: if bar and pair "connected", and pair on the right, OR bar and pair of different color, and pair on the left
• Jb: if bar and pair "connected", and pair on the left, OR bar and pair of different color, and pair on the right

A bar only

• One possible case: F.

A corner

• Possible cases are: Aa, Ab, or V.
• V: the opposite corners adjacent to the corner are of DIFFERENT color:
• Aa: The opposite corners have same color, and the one of the RIGHT is of opposite color compared to adjacent pair.
• Ab: The opposite corners have same color, and the one of the LEFT is of opposite color compared to adjacent pair.

Two pairs (without corner)

• Possible cases: Ja, Jb, Na, Nb, or Y'

In all cases but Y, we have either two RIGHT/LEFT stickers of same color + left/right sticker of either OPPOSITE or DIFFERENT color.

• Na: The stickers of same color are on the RIGHT, and the left sticker has the OPPOSITE color on EACH face.
• Nb: The stickers of same color are on the LEFT, and the left sticker has the OPPOSITE color on EACH face.
• Ja: The RIGHT sticker on the right face has a DIFFERENT color.
• Jb: The LEFT sticker on the left face has a DIFFERENT color.
• Y: Easily recognizable since both pairs are adjacent to a same corner.

Pair + headlight

• Possible cases: Aa, Ab, T, Ra, Rb, Ga, or Gc.
• Aa: Pair is on the RIGHT, and headlight has OPPOSITE color.
• Ab: Pair is on the LEFT, and headlight has OPPOSITE color.
• T: headlight and pair have a common corner, and the edge adjacent to headlight corner is OPPOSITE color.

TBC

A pair only

Two headlights

One headlight only

Nothing

• E perm if corner has one color identical to one side and one color opposite to the other side. Set up the case by moving the corner and side with identical color on the left or right side.